Capítulo 6 Análise de séries temporais
Qualquer conjunto de observações ordenadas no tempo são chamadas de Séries Temporais. No caso da Engenharia Ambiental e Urbana, podem ser citados alguns exemplos: valores diários de poluição, valores mensais de temperatura, temperaturas máximas e mínimas diárias ou precipitação atmosférica anual em uma cidade, entre outros (Morettin 2018).
É suposto que, em uma análise de série temporal, “há um sistema causal mais ou menos constante, relacionado com o tempo, que exerceu influência sobre os dados no passado e pode continuar a fazê-lo no futuro. Este sistema causal costuma atuar criando padrões não aleatórios que podem ser detectados em um gráfico da série temporal, ou mediante algum outro processo estatístico” (Reis 2022).
É importante citar que identificar esses padrões não aleatórios na série temporal de uma variável de interesse é o objetivo da análise. A partir dessa identificação, é possível realizar previsões, orientando tomadas de decisões na área de interesse (Reis 2022).
A partir de procedimentos estatísticos, é possível realizar a análise da série de dados de forma que seja possível realizar previsões, analisar causalidades e estudar periodicidades relevantes. Conforme COSTA (2022) e SOARES (2020), em resumo, nas séries temporais caracterizam-se por:
- Possuirem variáveis aleatórias;
- Observações altamente correlacionadas, principalmente porque medidas adjacentes (próximas no tempo) tendem a correlatas;
- Existência de fatores determinísticos, como tendência, sazonalidade e ciclos;
- Dificuldade em lidar com outliers;
- Mudanças fundamentais/abruptas.
De acordo com Reis (2022) e Barros, D., and D. (2017), séries temporais são compostas pelos seguintes padrões:
Tendência (T): série temporal que segue determinada direção, não necessariamente linear, podendo também ser crescente ou decrescente. Exemplos podem ser: crescimento demográfico, ou mudança gradual de hábitos de consumo, ou qualquer outro aspecto que afete a variável de interesse no longo prazo;
Variações cíclicas ou ciclos (C), flutuações nos valores da variável com duração superior a um ano, e que se repetem com certa periodicidade, que podem ser resultado de variações da economia como períodos de crescimento ou recessão, ou fenômenos climáticos como o El Niño (que se repete com periodicidade superior a um ano);
Variações sazonais ou sazonalidade (S), flutuações nos valores da variável com duração inferior a um ano, e que se repetem todos os anos, geralmente em função das estações do ano (ou em função de feriados ou festas populares, ou por exigências legais, como o período para entrega da declaração de Imposto de Renda); se os dados forem registrados anualmente NÃO haverá influência da sazonalidade na série;
Variações irregulares (I), que são as flutuações inexplicáveis, resultado de fatos inesperados como catástrofes naturais, decisões intempestivas de governos, etc.
Estes são estudados para controlar o efeito de cada componente a fim de analisar o comportamento de cada “série filtrada” e, ainda, analisar as particularidades de cada componente (COSTA, 2022).
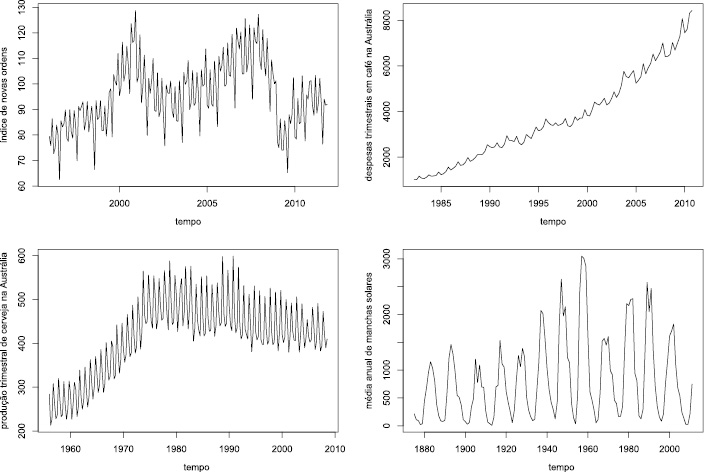
(#fig:figura 3.1)Figura 3.1: Séries exibindo diferentes tipos de padrões (Fonte: BARROS et. al, 2022)
De acordo com COSTA (2022), existem duas abordagens na análise de séries temporais:
Clássica: descreve o comportamento da série por meio de componentes não observáveis, ou seja, a tendência, sazonalidade e ciclo. Os desvios em torno dos valores determinísticos1 ocorrem por erros aleatórios e não pela natureza estocástica da série.
Moderna: supões que a série temporal seja formada por um processo estocástico2. Sendo cada observação composta por um conjunto de variáveis aleatórias, estas são representadas por funções de densidade individuais. Para capturar sua característica estocástica, são utilizadas modelos estatísticos.
References
Em um modelo determinístico, indepentemente dos conjuntos de entrada, o resultado será sempre o mesmo conjunto de saídas.↩︎
Processo estocástico: sequência de variáveis aleatórias cujas características probabilísticas não se alteram ao longo do tempo. Exemplo: No lançamento de dados cada face tem a mesma probabilidade de ficar para cima↩︎